Last week, we discussed a paradigm shift from linear to exponential. Today, we find out what that means. Let’s get right to business with this thought-provoking quote:
| “The greatest shortcoming of the human race is our inability to understand the exponential function.” – Prof. Al Bartlett |
Wow. That’s a pretty bold claim. But is it justified? I’ll let you decide for yourself, after we take a look at some examples.
One of the earliest and most famous recorded instances of the human brain underestimating the exponential function is encountered in the story of the man who invented the chessboard. The story goes that when the inventor presented the game to the ruler of the lands at the time, the ruler liked it so much that he allowed the inventor to name his own reward. The inventor, being a pretty clever guy and a mathematician, asked for a pay out in wheat grains. One grain on the first square of the chess board, two grains on the second, four on the third, eight on the fourth, and doubling again for each next square until the 64-square chessboard was filled.
To the ruler, mind mired in linear thinking, this seemed like a sensible reward. And indeed, while the first half of the chess board was being filled with wheat grains, nothing outrageous seemed to be happening. After doubling 32 times, the total number of grains amounted to 4,294,967,296 – which equals about 560,000kg. While the clever inventor was certain to never go hungry again, the ruler was very pleased with his new game and still felt like he’d struck a bargain. 
Then the 33rd square came along. The number of grains on this square was equal to the amount on all previous squares combined: 4,294,967,296. The total number of grains was now up to 8,589,934,592. The doubling continued. Each new square contained the same amount of grains as all previous squares combined. By the end of the exercise, it became clear that no ruler in the world could pay out such a reward. The total amount of grains required to fill the board was 18,446,744,073,709,551,615. This would result in a heap larger than Mount Everest. In some versions of this tale the inventor was beheaded, in others he was instantly made chief advisor to the ruler. The lesson is the same.
| “The greatest shortcoming of the human race is our inability to understand the exponential function.” |
Double time
Let’s investigate some more; consider the following problem:
| A beaker sits in a lab at 11:00, containing one bacterium. The bacteria double in number each minute. One hour later, the beaker is completely full. What is the time when the beaker is still half-empty? |
The answer may surprise you: The beaker is half empty at 11:59. To continue the mental exercise, let’s go back another five minutes. How full is the beaker at 11:54? The answer is a mere 3.125%. Six minutes before the bacteria run out of room, their environment consists of almost 97% unoccupied space.
Now say we want to keep growing the bacteria. How many extra beakers do we need to keep the exponential growth going, say, for another four minutes after the first beaker fills up? Well, at 12:01 there are two beakers worth of bacteria. One minute later, they double again. Four beakers. At 12:03, we need a total of eight beakers to hold everything. It’s now 12:04. The bacteria fill up 16 beakers.
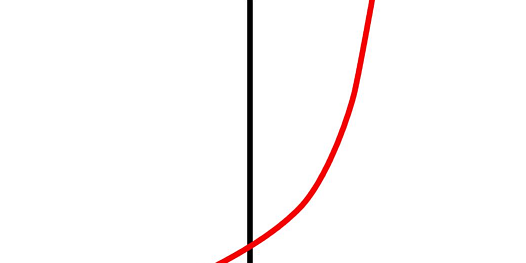
Mind boggled yet? Good, let’s backtrack once more. It takes 57 minutes to go from a single bacterium to an amount large enough to fill 3% of a single beaker. In the next 10 minutes, the exponential function hits the money zone, and takes the bacteria from a single beaker with 97% free space to 16 completely filled beakers. This part of an exponential curve is typically called the inflection point or the “knee in the curve”. Famous futurist Ray Kurzweil understandably calls this “the second half of the chessboard”.
And with that stunner we say goodbye – for now. Next week we put the magnifying glass to the information economy, and discover how the exponential function drives it. If you enjoyed this blog, make sure to subscribe to our Storybook on the right, share it on your social media of choice using the buttons below, and leave a comment. I look forward to hearing your thoughts.
See you next week!